задача з мого brainrot каналу по всьому що хоч частково алгебра.

в ABC вписано рівносторонній трикутник DEF, доведіть, що точка перетину кіл AEF, BFD, CDE не залежить від вибору точки D.

бажаю удачі підписникам на відборах на RMM, якщо хтось пише.

в трикутнику ABC проведена нагеліана AK. доведіть, що її кола тебо рівні.

пряма через точку перетину симедіан K, проходить через точки D, E, F на сторонах BC, CA, AB трикутника ABC. BE і CF, CF і AD, AD і BE перетинаються в P, Q, R. доведіть, що точка інцидентності X прямих AP, BQ, CR належить описаному колу.

хз, наскільки баян, скоріше всього є в акопяні-заславському, ну в etc як мінімум. OH, T{1}Ap{1}, T{2}Ap{2} паралельні між собою.

коніка з фокусами в B, C перетинає AB в K і N, AC в L і M. BL і CK, BM і CN перетинаються в P, Q. доведіть, що прямі AP і AQ ізотомічно спряжені.

проста авторська
ABC - правильний. P - довільна точка площини. M - середина AB, W - середина дуги AB. CP перетинає (ABC) в точці X. Q - точка перетину (CXM) і AB - Q.R - (PXW) і (PBC). доведіть, що P, Q, R колінеарні.

"вечірній гроб"
дано правильний n-кутник A{1}A{2}...A{n}, його описане коло ω і довільна точка P. прямі A{1}P, A{2}P,...,A{n}P перетинають ω у B{1}, B{2},...,B{n}. доведіть, що у многокутник B{1}B{2}...B{n} можна вписати коніку.

надобраніч

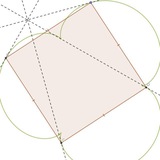
до вписаного чотирикутника ABCD проведено прямі PA, PB, PC, PD, які перетинають його описане коло в E, F, G, H. доведіть, що точки перетину діагоналей M і N цих 4кутників колінеарні з P.

досить корисна лема.
дано трикутник ABC його інцентр - I, центр зовнівписаного кола I_A, і ізогонально спряжені точки P і Q. тоді точки B, C, I, I_A, P, Q лежать на одній коніці.

і ще одна. G - центроїд ABC, A' доповнює до паралелограма. P і Q ізотомічно спряжені. із цього слідує, що B, C, G, A', P, Q лежать на одній коніці.

в чаті олімпіадної геометрії сплив один факт про точки дотику вписаних кіл прямокутного трикутника, ось більш загальне твердження для довільного трикутника.
пунктирні криві - коніки.
напевно баян як завжди)))

ну тут ще така шиза є. довго думав чи постити, но точка перетину хороша. X(64)

але це для таких конік. для інших там якась X(N) N>1000.

в трикутник ABC вписано дві коніки. зелена дотикається до BC в P, а червона в Q. AP перетинає червону в N, AQ зелену в M, доведіть, що дотичні в цих точках перетинаються на BC.

простенька задачка спеціально для тих хто поставив губи і пігулки на попередній пост.
перпендикуляр із B до дотичної в C і із C до дотичної в B перетинаються в D. доведіть, що AD містить центр кола 9 точок.

назвемо ортотрансверсальним спряженням точки P відносно ABC - другу точку перетину кіл (APA_{1}), (BPB_{1}), (CPC_{1}).
1.доведіть що ці кола завжди співвісні
2.доведіть, якщо P належить колу 9 точок, то P' описаному колу.

p. s. поправте мене, якщо у цього спряження є інша назва.

у трикутників ABC і DEF спільне описане коло. доведіть, що H_{ABC}H_{DEF} паралельно G_{ABC}G_{DEF}.