group-telegram.com/gonzo_ML/1146
Last Update:
[DeepMind AlphaTensor] Discovering faster matrix multiplication algorithms with reinforcement learning
Alhussein Fawzi, Matej Balog, Aja Huang, Thomas Hubert, Bernardino Romera-Paredes, Mohammadamin Barekatain, Alexander Novikov, Francisco J. R. Ruiz, Julian Schrittwieser, Grzegorz Swirszcz, David Silver, Demis Hassabis & Pushmeet Kohli
Статья: https://www.nature.com/articles/s41586-022-05172-4
Пост: https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor
Код: https://github.com/deepmind/alphatensor (только найденные алгоритмы и сопутствующее)
После статьи уже прошло сколько-то времени, но она важная, надо разобрать.
В этот раз подход AlphaGo (точнее его вариант Sampled AlphaZero для пространств действий высокой размерности, https://proceedings.mlr.press/v139/hubert21a) применили к задаче нахождения эффективного алгоритма для перемножения матриц.
Перемножение матриц везде вокруг. Без него никуда в компьютерной графике, обработке сигналов, научных вычислениях. Почти любой векторизованный алгоритм использует какое-то перемножение матриц. Злые языки также утверждают, что весь современный ИИ — это перемножение матриц. Наверное, эти кучки атомов просто завидуют. Получается, ускорение алгоритмов для перемножения матриц ускоряет всё вокруг.
Классический ручной алгоритм перемножения матриц, как его учат в школе-институте, прямолинейный и неэффективный, его сложность O(n^3) операций умножения, а в типовых процессорах это более дорогая операция, чем сложение. Для матриц 2x2 это соответственно 8 умножений. В 1969-м году Штрассен показал, что этот алгоритм неоптимален и предложил алгоритм с 7 умножениями. С тех пор понеслось, и учёные пытаются подобраться к квадратичному алгоритму, текущая SoTA O(n^2.37286) (https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/). Перебрать все возможные алгоритмы нереально, пространство огромно, поэтому поиск нужно делать по-умному.
Интересна репрезентация проблемы. Задача перемножения матриц заданной размерности сводится к тензорам особого вида (matrix multiplication tensor или Strassen’s tensor), которые могут описывать любую билинейную операцию (то есть бинарную операцию, линейную по каждому из аргументов), каковым перемножение матриц и является.
Кстати, хорошая статья “Tensors in computations” (https://www.stat.uchicago.edu/~lekheng/work/acta.pdf) про тензоры есть в предпоследнем Acta Numerica (https://www.cambridge.org/core/journals/acta-numerica). Там вообще хорошие статьи регулярно, следите за ними. В том же номере 2021 года (https://www.cambridge.org/core/journals/acta-numerica/volume/6A0DA33B45D0E5A6BABD1EF331B5E4F0), кстати, есть и известная статья Михаила Белкина, да и много другого интересного.
Тензор, описывающий произведение любых матриц n×n имеет размерность n^2 × n^2 × n^2 и содержит {0, 1}. Этот тензор описывает какие элементы из входных матриц брать, и куда писать результат. Например, для операции c1 = a1*b1 + a2*b3, где ai, bi, ci — элементы квадратных матриц A, B и C, элементы которых пронумерованы от единицы до макс.индекса слева-направо и сверху-вниз, в единицу выставляются элементы тензора с индексами (a1, b1, c1) и (a2, b3, c1).
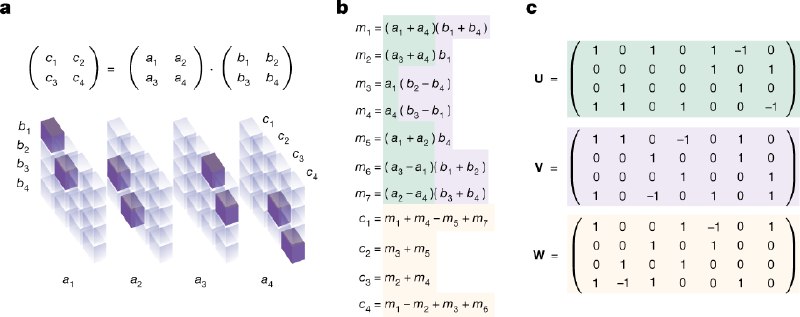
Когда есть такой тензор, то его можно декомпозировать в сумму R outer products векторов (тензоров ранга 1) u,v,w, и каждая декомпозиция будет очередным рецептом, как именно выполнить умножение матриц, а число термов в этой сумме, R, будет числом операций умножения в данном рецепте. Таким образом, задача поиска алгоритма перемножения матриц сводится к задаче поиска по декомпозициям соответствующего тензора.
BY gonzo-обзоры ML статей
Share with your friend now:
group-telegram.com/gonzo_ML/1146
