Чем больше цифра, тем меньше вероятность того, что она будет первой в числе.
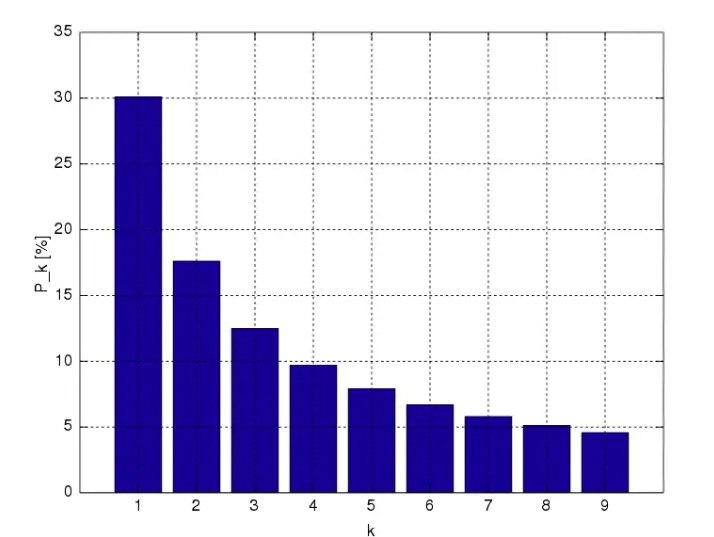
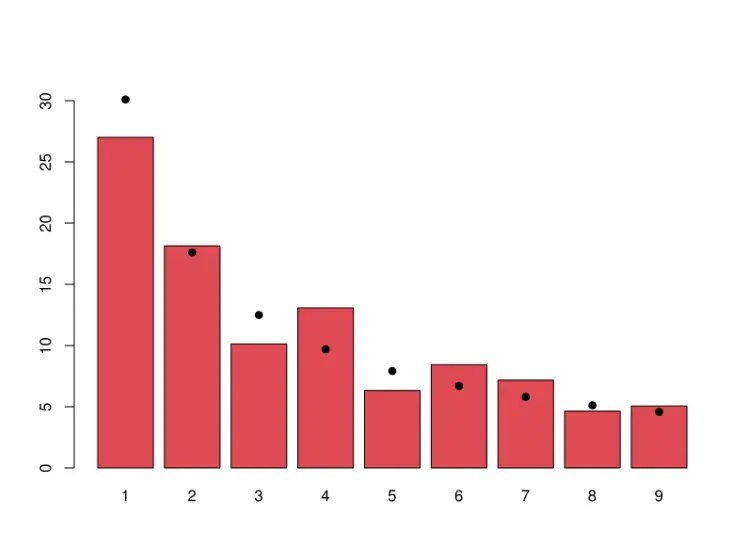
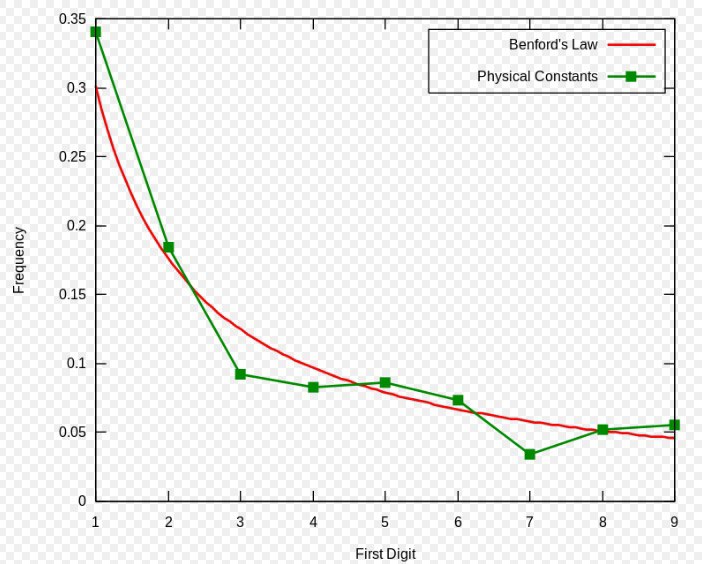
Закон Бенфорда гласит, что в реальных числовых данных ведущая цифра чаще всего малая. Например, вероятность того, что число начнется с 1, составляет около 30%, тогда как 9 встречается в качестве первой цифры менее чем в 5% случаев. Если бы цифры распределялись равномерно, каждая появлялась бы с вероятностью 11,1%. Примечательно, что даже последовательность Фибоначчи подчиняется этому закону.
Возьмем первые 15 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Ведущая цифра 1 встречается в 4 случаях из 15, с вероятностью 26,67%
Возьмем первые 30 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229. Ведущая цифра 1 встречается в 9 случаях из 30. Следовательно, вероятность теперь равна 30%.
💡Этот закон применим для выявления фальсификаций в данных. Например, правительство Греции было уличено в подделке макроэкономической статистики перед вступлением в еврозону после проверки данных по закону Бенфорда.
Закон Бенфорда гласит, что в реальных числовых данных ведущая цифра чаще всего малая. Например, вероятность того, что число начнется с 1, составляет около 30%, тогда как 9 встречается в качестве первой цифры менее чем в 5% случаев. Если бы цифры распределялись равномерно, каждая появлялась бы с вероятностью 11,1%. Примечательно, что даже последовательность Фибоначчи подчиняется этому закону.
Возьмем первые 15 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Ведущая цифра 1 встречается в 4 случаях из 15, с вероятностью 26,67%
Возьмем первые 30 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229. Ведущая цифра 1 встречается в 9 случаях из 30. Следовательно, вероятность теперь равна 30%.
💡Этот закон применим для выявления фальсификаций в данных. Например, правительство Греции было уличено в подделке макроэкономической статистики перед вступлением в еврозону после проверки данных по закону Бенфорда.
👍10🤪5😱4
group-telegram.com/hzinfomap/149
Create:
Last Update:
Last Update:
Чем больше цифра, тем меньше вероятность того, что она будет первой в числе.
Закон Бенфорда гласит, что в реальных числовых данных ведущая цифра чаще всего малая. Например, вероятность того, что число начнется с 1, составляет около 30%, тогда как 9 встречается в качестве первой цифры менее чем в 5% случаев. Если бы цифры распределялись равномерно, каждая появлялась бы с вероятностью 11,1%. Примечательно, что даже последовательность Фибоначчи подчиняется этому закону.
Возьмем первые 15 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Ведущая цифра 1 встречается в 4 случаях из 15, с вероятностью 26,67%
Возьмем первые 30 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229. Ведущая цифра 1 встречается в 9 случаях из 30. Следовательно, вероятность теперь равна 30%.
💡Этот закон применим для выявления фальсификаций в данных. Например, правительство Греции было уличено в подделке макроэкономической статистики перед вступлением в еврозону после проверки данных по закону Бенфорда.
Закон Бенфорда гласит, что в реальных числовых данных ведущая цифра чаще всего малая. Например, вероятность того, что число начнется с 1, составляет около 30%, тогда как 9 встречается в качестве первой цифры менее чем в 5% случаев. Если бы цифры распределялись равномерно, каждая появлялась бы с вероятностью 11,1%. Примечательно, что даже последовательность Фибоначчи подчиняется этому закону.
Возьмем первые 15 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Ведущая цифра 1 встречается в 4 случаях из 15, с вероятностью 26,67%
Возьмем первые 30 чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229. Ведущая цифра 1 встречается в 9 случаях из 30. Следовательно, вероятность теперь равна 30%.
💡Этот закон применим для выявления фальсификаций в данных. Например, правительство Греции было уличено в подделке макроэкономической статистики перед вступлением в еврозону после проверки данных по закону Бенфорда.
BY ХЗ Инфо | Карты и статистика

Share with your friend now:
group-telegram.com/hzinfomap/149
