шиза напевно. ортотрансверсаль інцентра - триполяра X(57).

доведіть, що парабола, що проходить через B, C, I, I_A дотикається до описаного кола ABC.

p. s. знаю що це вже було в каналі, но може хтось знайде гарне рішення без кубік.

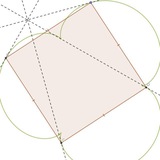
ну і знову задача про вписані параболи.
дано дві діаметрально протилежні точки P і Q на (BIC), проведено параболи Ω_1 і Ω_2 через B, C, P, Q.
1. доведіть, що Ω_1 і Ω_2 дотикаються до (ABC).
2. якщо M і N точки дотику, то доведіть, що вони діаметрально протилежні.

думаю знову ж таки баян на теорему нілова.


невеличка поправка. червоні кути не між параболами, а між хордами кола (BIC)

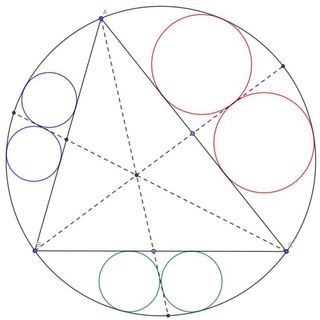
(!) Вписаний еліпс з фокусами у ортоцентрі та центрі описаного кола дотикається до кола Ейлера

H - ортоцентр ABC. точки дотику вписаних кіл HBC, HCA, HAB до BC, CA, AB - D, E, F. доведіть, що прямі AD, BE, CF перетинаються в одній точці.

я ненавиджу geogebra 5. я зробив досить точну приблизну побудову, а виявляється факт не правдивий. найбільш залайкана задача - фейк. більше не поститиму задач в 3 ночі. вибачте, підписники.

а ще я не знаю як забрати цю "задачу" з аватарки каналу.

розминка. тримайте щось просте і добре на ранок.
в трапеції ABCD зелене коло через AB дотикається до CD в P. доведіть, що (ADP) і (BCP) перетинаються на AB.

хоча, вона запроста. пропоную тоді вирішити через додавання точок на кубиці.

думаю це відомий факт, але виглядає прикольно. через A, B ,C, O, H провели гіперболу і вибрали на ній точку X. прямі AX, BX, CX перетинають описане коло в D, E, F які відобразили відносно BC, CA, AB отримавши D', E', F'. доведіть, що трикутники ABC і D'E'F' перспективні.

точки A, B, C відобразили відносно BC, CA, AB отримавши A', B', C'. якщо I_A, I_B, I_C центри відповідних зовнівписаних кіл, то доведіть, що A'I_A, B'I_B, C'I_C проходять через одну точку

ну і дещо із старих конструкцій.
доведіть, що ізогональне спряження P лежить на середній лінії до основи BC.

цікаво чи через 255 рішається, хоча може просто схоже.

ранковий баян. кола (AXI_A), (BXI_B), (CXI_C) завжди співвісні.

точка P така, що її чевіанний трикутник DEF рівносторонній. T - центр DEF, O - центр описаного кола ABC. доведіть, що Т, O, P колінеарні.

до речі, хтось знає ще якісь властивості точки P?

довго думав чи викладати, но виглядає гарно.
чевіанний трикутник DEF точки P - рівносторонній, (DEF) перетинає сторони трикутника вдруге у K, L, M, відповідні чевіани AK, BL, CM перетинаються в R(очевидно із степені точки). Q - ізогональне спряження P. доведіть, що P, Q, R - одна пряма.

не люблю такі задачі, но...

N - точка нагеля. доведіть, що P, Q, R на одній прямій.

ось вам трохи класики.
точки без позначок - середини сторін.
P, Q - перетини двох червоних і зелених кіл.
G - центр мас A, B, C, D.
доведіть, що відмічені точки колінеарні.

коніку що проходить через вершини B, C ізогонально відобразили відносно ABC
1. доведіть, що її образ - також коніка
2. якщо один із фокусів був в точці A, то доведіть, що він зберігся

придумайте хтось узагальнення, пж, бо мені лінь

AD - бісектриса, I1, I2 - центри вписаних кіл ABD, ACD.
Довести, що I1I2 та зовнішня бісектриса кута А перетинаються на BC.