скучні задачі
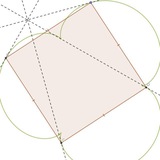
AD - бісектриса, I1, I2 - центри вписаних кіл ABD, ACD. Довести, що I1I2 та зовнішня бісектриса кута А перетинаються на BC.
узагальнення 😈.
AP і AQ - ізогоналі. I_1, I_2 - центри вписаних кіл ABP і ACQ.
доведіть, що лінія центрів цих кіл проходить через зовнішню бісектрису кута A.
AP і AQ - ізогоналі. I_1, I_2 - центри вписаних кіл ABP і ACQ.
доведіть, що лінія центрів цих кіл проходить через зовнішню бісектрису кута A.
здається давно не було задач на побудову.
A, B, C - точки коніки Г, F_1, F_2 - фокуси. побудуйте F_2, якщо всі інші точки дано.
A, B, C - точки коніки Г, F_1, F_2 - фокуси. побудуйте F_2, якщо всі інші точки дано.
скучні задачі
здається давно не було задач на побудову. A, B, C - точки коніки Г, F_1, F_2 - фокуси. побудуйте F_2, якщо всі інші точки дано.
попередня задача якась складна. тоді пропоную таку.
побудуйте фокус вписаної в ABC параболи по перспектору
побудуйте фокус вписаної в ABC параболи по перспектору
Точка A
Пряма l крізь точку A
точка S напевно не на прямій l
Якийсь відрізок k
Побудувати точки B, C на l такі що кут BSC прямий і AB*AC=k^2
Пряма l крізь точку A
точка S напевно не на прямій l
Якийсь відрізок k
Побудувати точки B, C на l такі що кут BSC прямий і AB*AC=k^2
на 100 підписників чекайте невеличку статтю про синтетику епіциклоїд
поризм мікеля, або ботанський погляд на поворотну гомотетію . дано n кіл ω_1, ω_2,...,ω_n що проходять через одну точку O. вторинні точки перетину(між ω_1 і ω_2, ..., ω_n і ω_1) позначимо як P_1, P_2,..., P_n. A_1 - довільна точка на ω_1, A_2 - точка перетину A_1P_1 і ω_2,..., доведіть, що точки P_{n+1} і P_1 співпадають
це не задача, а просто спостереження таке тривіальне.
це не задача, а просто спостереження таке тривіальне.
#задача_на_побудову
дано трикутник ABC і довільну точку P. побудуйте X такий на (ABC), що пряма XY проходить через P, де Y - ізогональне спряження X.
дано трикутник ABC і довільну точку P. побудуйте X такий на (ABC), що пряма XY проходить через P, де Y - ізогональне спряження X.
скучні задачі
risnobiy_the_boring_problems.pdf
це коллаб, який не вдався. мало бути в математиці лфмл, але автор сказав, що це поки ще заскладно і не в тему. тому, учням лфмл, та й всім охочим пропоную повирішувати цей різнобій. якщо є питання по задачах чи бажання себе перевірити, то пишіть мені @don_schijuan
скучні задачі
це коллаб, який не вдався. мало бути в математиці лфмл, але автор сказав, що це поки ще заскладно і не в тему. тому, учням лфмл, та й всім охочим пропоную повирішувати цей різнобій. якщо є питання по задачах чи бажання себе перевірити, то пишіть мені @don_schijuan
а і ще дещо. в неділю буде розбір різнобою.