Warning: file_put_contents(aCache/aDaily/post/botgeom/-221-222-): Failed to open stream: No space left on device in /var/www/group-telegram/post.php on line 50
Ботаем геому | Telegram Webview: botgeom/222 -
Telegram Group & Telegram Channel
Telegram Group » United States » Ботаем геому » Telegram Webview » Post 222
Ботаем геому
Две похожие задачи с немного похожими решениями

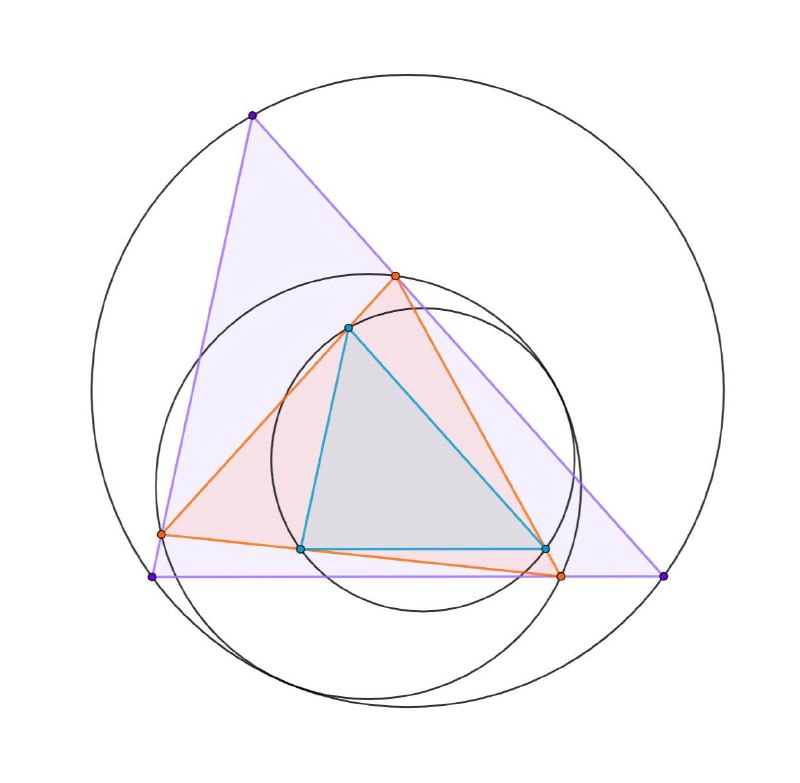
1. (Ол ЮМШ 2024 10-11) Три треугольника таковы, что второй вписан в первый, третий вписан во второй и гомотетичен первому.
(!) Если описанные окружности первого и второго касаются, то и описанные окружности второго и третьего тоже касаются

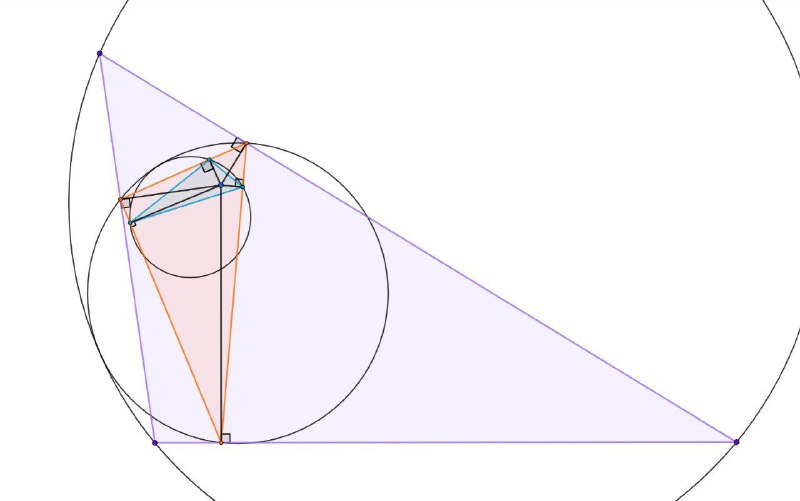
2. Три треугольника таковы, что второй – педальный треугольник некоторой точки относительно первого, а третий – педальный треугольник той же точки относительной второго.
(!) То же, что и в первой задаче

upd. Вторая задача является следствием первой, но есть красивое решение, работающие только для второй задачи
www.group-telegram.com/us/botgeom.com/222
741 viewsТихомир Листожуй 🐳, 



group-telegram.com/botgeom/222
Create:
Last Update:

Две похожие задачи с немного похожими решениями

1. (Ол ЮМШ 2024 10-11) Три треугольника таковы, что второй вписан в первый, третий вписан во второй и гомотетичен первому.
(!) Если описанные окружности первого и второго касаются, то и описанные окружности второго и третьего тоже касаются

2. Три треугольника таковы, что второй – педальный треугольник некоторой точки относительно первого, а третий – педальный треугольник той же точки относительной второго.
(!) То же, что и в первой задаче

upd. Вторая задача является следствием первой, но есть красивое решение, работающие только для второй задачи

BY Ботаем геому





Share with your friend now:
group-telegram.com/botgeom/222

View MORE
Open in Telegram


Telegram | DID YOU KNOW?

Date: |

After fleeing Russia, the brothers founded Telegram as a way to communicate outside the Kremlin's orbit. They now run it from Dubai, and Pavel Durov says it has more than 500 million monthly active users. "Your messages about the movement of the enemy through the official chatbot … bring new trophies every day," the government agency tweeted. At this point, however, Durov had already been working on Telegram with his brother, and further planned a mobile-first social network with an explicit focus on anti-censorship. Later in April, he told TechCrunch that he had left Russia and had “no plans to go back,” saying that the nation was currently “incompatible with internet business at the moment.” He added later that he was looking for a country that matched his libertarian ideals to base his next startup. These administrators had built substantial positions in these scrips prior to the circulation of recommendations and offloaded their positions subsequent to rise in price of these scrips, making significant profits at the expense of unsuspecting investors, Sebi noted. The company maintains that it cannot act against individual or group chats, which are “private amongst their participants,” but it will respond to requests in relation to sticker sets, channels and bots which are publicly available. During the invasion of Ukraine, Pavel Durov has wrestled with this issue a lot more prominently than he has before. Channels like Donbass Insider and Bellum Acta, as reported by Foreign Policy, started pumping out pro-Russian propaganda as the invasion began. So much so that the Ukrainian National Security and Defense Council issued a statement labeling which accounts are Russian-backed. Ukrainian officials, in potential violation of the Geneva Convention, have shared imagery of dead and captured Russian soldiers on the platform.
from us



Warning: filemtime(): stat failed for aCache/aDaily/post/botgeom/-221-222- in /var/www/group-telegram/post.php on line 310

Warning: filemtime(): stat failed for aCache/aDaily/post/botgeom/-221-222- in /var/www/group-telegram/post.php on line 311

Две похожие задачи с немного похожими решениями

 Ботаем геому TG
Webview: 222
Ботаем геому.Telegram Webview
Ботаем геому Telegram TG Channel
Telegram Updated:
Telegram Ботаем геому
FROM American