Как доказывать касание окружностей
Начнем небольшую серию постов, в которой рассмотрим полезные мысли и леммы, помогающие доказывать касание окружностей, и научимся их применять
Мысли:
1. Чаще всего точка касания угадывается. Почти всегда причиной касания является то, что нужные нам окружности просто всегда имеют хорошую общую точку, но нам повезло, и углы такие, что окружности коснулись. А как искать хорошую точку на описанной окружности треугольника? Например, можно взять 3 прямые, содержащие стороны этого треугольника, добавить к ним четвертую прямую и рассмотреть точку Микеля этой четвёрки. Через неё как раз пройдёт 4 окружности, которые помогут поперекидывать углы. Только четвёртую прямую нужно выбирать более менее нормальную.
*Ещё иногда точкой касания является антиштейнер какой то хорошей прямой. Если нет явно заданной прямой через Н, то антиштейнер прямой заданного направления. Вайб такого случая это отражения точек/прямых относительно сторон базового треугольника или явная прямая через Н.
2. Также бывает более глубокая причина касания окружностей, чем уголки. Иногда можно получить касающиеся окружности из уже касающихся объектов на рисунке с помощью поворотной гомотетии или инверсии.
3. Можно попробовать найти на картинке теорему Фейербаха (или какие-то другие известные касания).
Леммы:
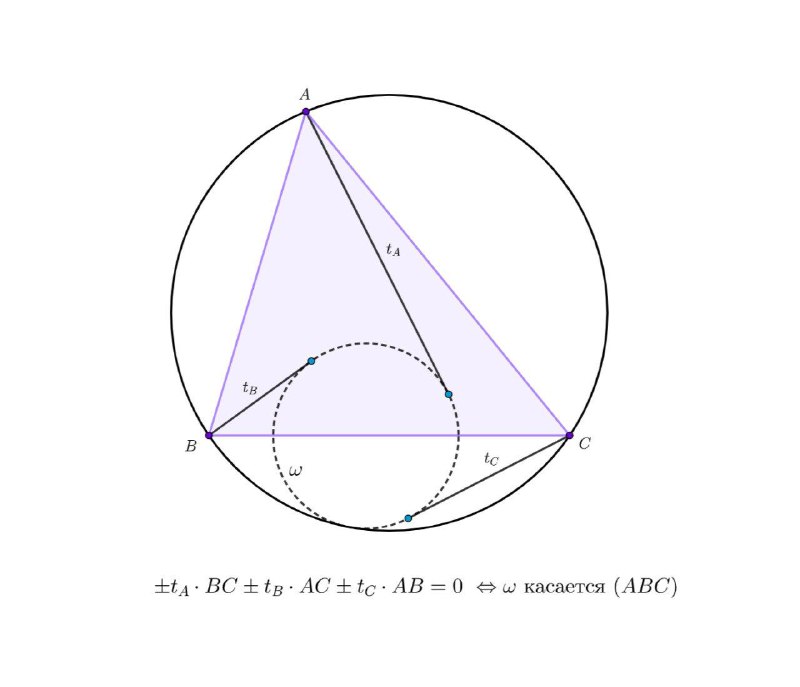
1. Слабая теорема Кейси (Кузи) (рис. 1)
Пусть на плоскости даны окружность ω и три точки A, B, C вне неё, не лежащие на одной прямой. Обозначим
длины отрезков касательных из точек A, B, C к окружности ω через ta, tb, tc соответственно. Тогда окружность (ABC) касается окружности ω тогда и только тогда, когда для некоторой расстановки знаков выполнено соотношение
±taBC ± tbCA ± tcAB = 0
Полезно, когда считаются отрезки или явно фигурируют касательные.
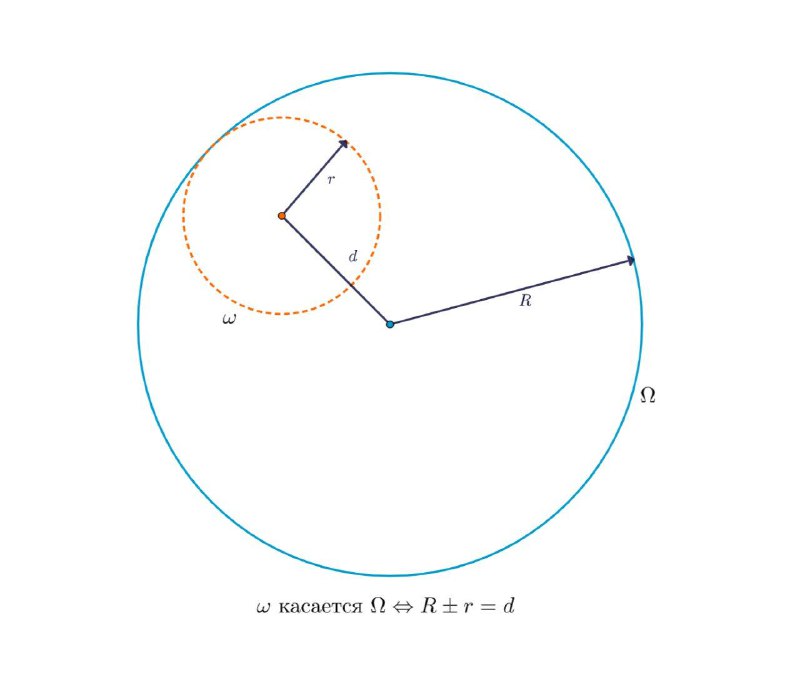
2. Очев лемма (рис. 2)
Окружности касаются тогда только тогда, когда Сумма/разность радусов = расстояние между их центрами.
Работает, когда ничего больше не работает. Обычно в таких задачах удобно считаются радиусы окружностей.
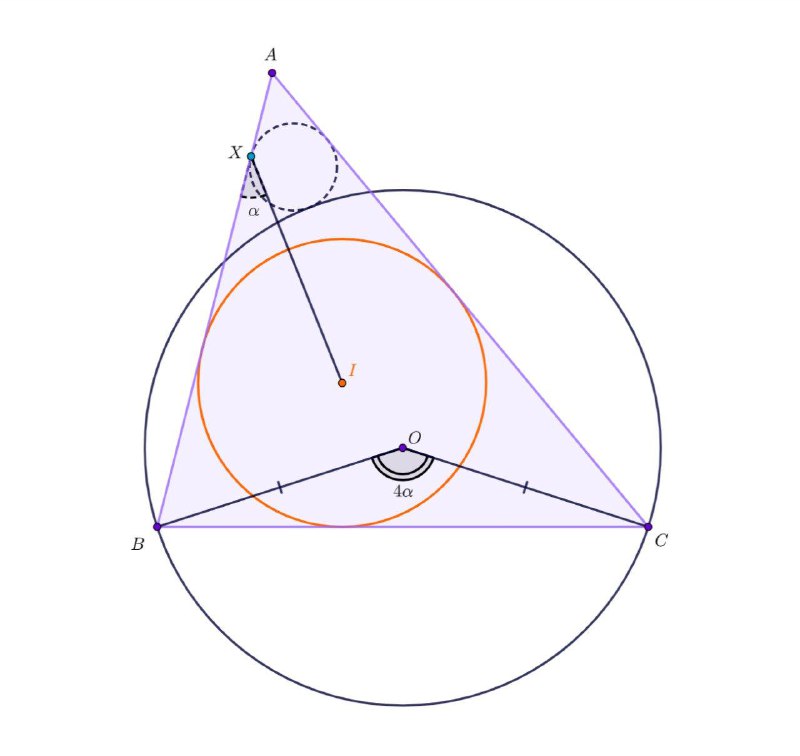
3. Лемма о сегменте (рис. 3)
Точка I – инцентр треугольника ABC. Окружность ω с центром в точке O проходит через вершины B и C. Точка Х на AB такова, что ∠BXI = ¼∠BOC. Тогда окружность, вписанная в угол A и касающаяся стороны АВ в точке X, касается ω.
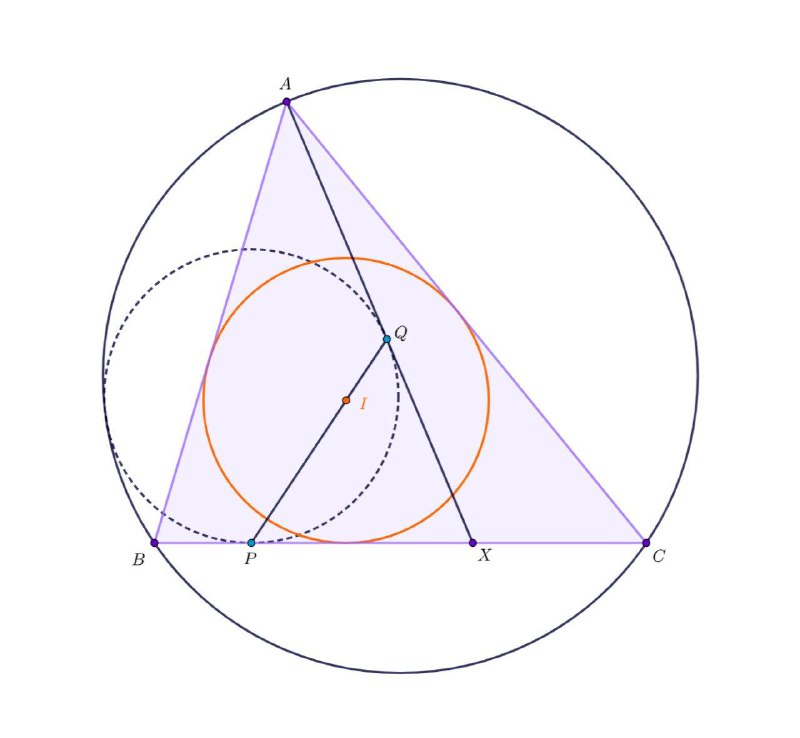
4. Лемма Саваямы (рис. 4)
На стороне BC треугольника ABC выбрана точка X. Тогда окружность, вписанная в угол BXA и касающаяся его сторон в точках P и Q, касается (ABC) тогда и только тогда, когда PQ содержит инцентр (или эксцентр) треугольника АВС.
Полезно подумать о том, что точка Х выбрана не совсем "симметрично". И получить ещё несколько фактов.
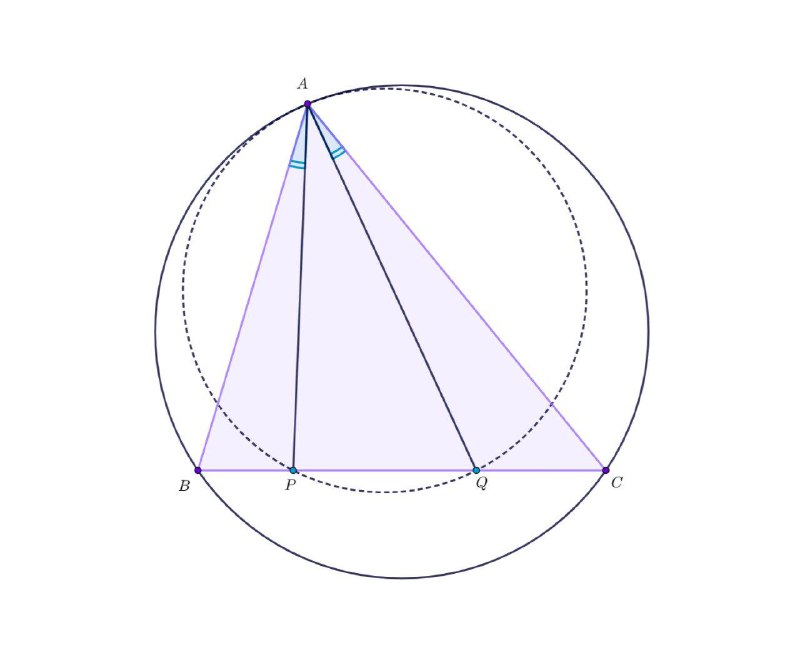
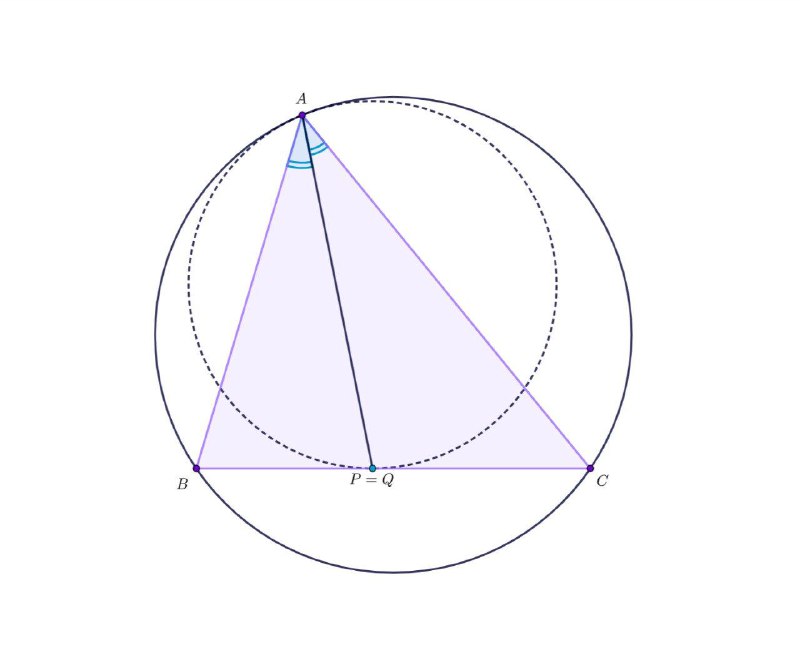
5. Лемма с изогоналями (обобщение леммы Архимеда) (рис. 5-6)
Иногда удобнее доказывать изогональность или что какая-то прямая является биссектрисой (например, с помощью счета отрезков), вместо того, чтобы искать угол между касательной и хордой.
Ещё у неё есть прикольное обобщение.
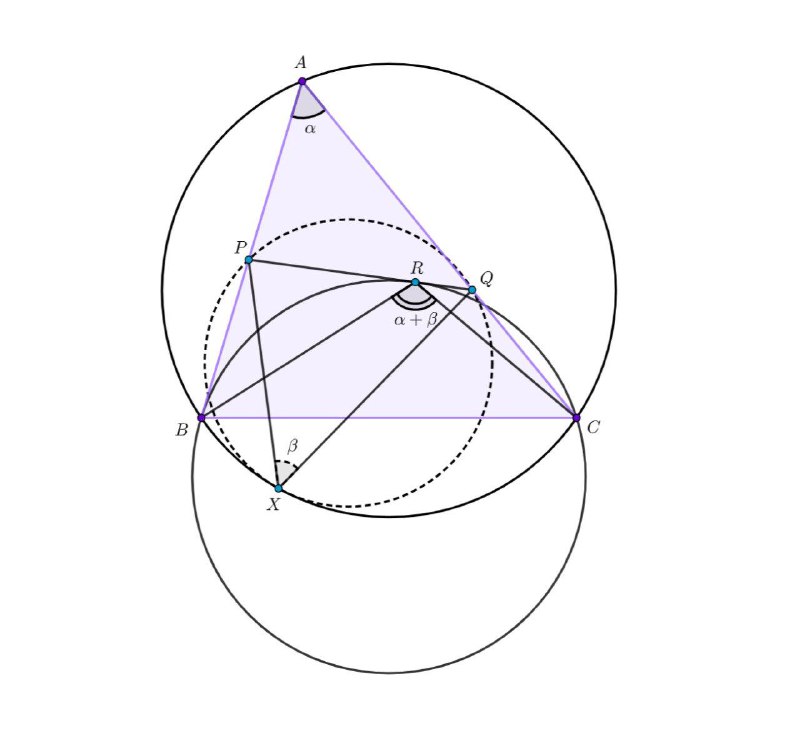
6. Полезная лемма без названия (рис. 7)
Внутри треугольника ABC выбрана точка R. Касательная к (BRC) пересекает стороны AB и AC в точках P и Q соответственно. Точка Х находится на дуге BC, не содержащей точку А. Утверждается, что (PXQ) касается (ABC) тогда и только тогда, когда ∠BAC + ∠PXQ = ∠BRC
Узнал про неё отсюда.
Начнем небольшую серию постов, в которой рассмотрим полезные мысли и леммы, помогающие доказывать касание окружностей, и научимся их применять
Мысли:
1. Чаще всего точка касания угадывается. Почти всегда причиной касания является то, что нужные нам окружности просто всегда имеют хорошую общую точку, но нам повезло, и углы такие, что окружности коснулись. А как искать хорошую точку на описанной окружности треугольника? Например, можно взять 3 прямые, содержащие стороны этого треугольника, добавить к ним четвертую прямую и рассмотреть точку Микеля этой четвёрки. Через неё как раз пройдёт 4 окружности, которые помогут поперекидывать углы. Только четвёртую прямую нужно выбирать более менее нормальную.
*Ещё иногда точкой касания является антиштейнер какой то хорошей прямой. Если нет явно заданной прямой через Н, то антиштейнер прямой заданного направления. Вайб такого случая это отражения точек/прямых относительно сторон базового треугольника или явная прямая через Н.
2. Также бывает более глубокая причина касания окружностей, чем уголки. Иногда можно получить касающиеся окружности из уже касающихся объектов на рисунке с помощью поворотной гомотетии или инверсии.
3. Можно попробовать найти на картинке теорему Фейербаха (или какие-то другие известные касания).
Леммы:
1. Слабая теорема Кейси (Кузи) (рис. 1)
Пусть на плоскости даны окружность ω и три точки A, B, C вне неё, не лежащие на одной прямой. Обозначим
длины отрезков касательных из точек A, B, C к окружности ω через ta, tb, tc соответственно. Тогда окружность (ABC) касается окружности ω тогда и только тогда, когда для некоторой расстановки знаков выполнено соотношение
±taBC ± tbCA ± tcAB = 0
Полезно, когда считаются отрезки или явно фигурируют касательные.
2. Очев лемма (рис. 2)
Окружности касаются тогда только тогда, когда Сумма/разность радусов = расстояние между их центрами.
Работает, когда ничего больше не работает. Обычно в таких задачах удобно считаются радиусы окружностей.
3. Лемма о сегменте (рис. 3)
Точка I – инцентр треугольника ABC. Окружность ω с центром в точке O проходит через вершины B и C. Точка Х на AB такова, что ∠BXI = ¼∠BOC. Тогда окружность, вписанная в угол A и касающаяся стороны АВ в точке X, касается ω.
4. Лемма Саваямы (рис. 4)
На стороне BC треугольника ABC выбрана точка X. Тогда окружность, вписанная в угол BXA и касающаяся его сторон в точках P и Q, касается (ABC) тогда и только тогда, когда PQ содержит инцентр (или эксцентр) треугольника АВС.
Полезно подумать о том, что точка Х выбрана не совсем "симметрично". И получить ещё несколько фактов.
5. Лемма с изогоналями (обобщение леммы Архимеда) (рис. 5-6)
Иногда удобнее доказывать изогональность или что какая-то прямая является биссектрисой (например, с помощью счета отрезков), вместо того, чтобы искать угол между касательной и хордой.
Ещё у неё есть прикольное обобщение.
6. Полезная лемма без названия (рис. 7)
Внутри треугольника ABC выбрана точка R. Касательная к (BRC) пересекает стороны AB и AC в точках P и Q соответственно. Точка Х находится на дуге BC, не содержащей точку А. Утверждается, что (PXQ) касается (ABC) тогда и только тогда, когда ∠BAC + ∠PXQ = ∠BRC
Узнал про неё отсюда.
group-telegram.com/botgeom/328
Create:
Last Update:
Last Update:
Как доказывать касание окружностей
Начнем небольшую серию постов, в которой рассмотрим полезные мысли и леммы, помогающие доказывать касание окружностей, и научимся их применять
Мысли:
1. Чаще всего точка касания угадывается. Почти всегда причиной касания является то, что нужные нам окружности просто всегда имеют хорошую общую точку, но нам повезло, и углы такие, что окружности коснулись. А как искать хорошую точку на описанной окружности треугольника? Например, можно взять 3 прямые, содержащие стороны этого треугольника, добавить к ним четвертую прямую и рассмотреть точку Микеля этой четвёрки. Через неё как раз пройдёт 4 окружности, которые помогут поперекидывать углы. Только четвёртую прямую нужно выбирать более менее нормальную.
*Ещё иногда точкой касания является антиштейнер какой то хорошей прямой. Если нет явно заданной прямой через Н, то антиштейнер прямой заданного направления. Вайб такого случая это отражения точек/прямых относительно сторон базового треугольника или явная прямая через Н.
2. Также бывает более глубокая причина касания окружностей, чем уголки. Иногда можно получить касающиеся окружности из уже касающихся объектов на рисунке с помощью поворотной гомотетии или инверсии.
3. Можно попробовать найти на картинке теорему Фейербаха (или какие-то другие известные касания).
Леммы:
1. Слабая теорема Кейси (Кузи) (рис. 1)
Пусть на плоскости даны окружность ω и три точки A, B, C вне неё, не лежащие на одной прямой. Обозначим
длины отрезков касательных из точек A, B, C к окружности ω через ta, tb, tc соответственно. Тогда окружность (ABC) касается окружности ω тогда и только тогда, когда для некоторой расстановки знаков выполнено соотношение
±taBC ± tbCA ± tcAB = 0
Полезно, когда считаются отрезки или явно фигурируют касательные.
2. Очев лемма (рис. 2)
Окружности касаются тогда только тогда, когда Сумма/разность радусов = расстояние между их центрами.
Работает, когда ничего больше не работает. Обычно в таких задачах удобно считаются радиусы окружностей.
3. Лемма о сегменте (рис. 3)
Точка I – инцентр треугольника ABC. Окружность ω с центром в точке O проходит через вершины B и C. Точка Х на AB такова, что ∠BXI = ¼∠BOC. Тогда окружность, вписанная в угол A и касающаяся стороны АВ в точке X, касается ω.
4. Лемма Саваямы (рис. 4)
На стороне BC треугольника ABC выбрана точка X. Тогда окружность, вписанная в угол BXA и касающаяся его сторон в точках P и Q, касается (ABC) тогда и только тогда, когда PQ содержит инцентр (или эксцентр) треугольника АВС.
Полезно подумать о том, что точка Х выбрана не совсем "симметрично". И получить ещё несколько фактов.
5. Лемма с изогоналями (обобщение леммы Архимеда) (рис. 5-6)
Иногда удобнее доказывать изогональность или что какая-то прямая является биссектрисой (например, с помощью счета отрезков), вместо того, чтобы искать угол между касательной и хордой.
Ещё у неё есть прикольное обобщение.
6. Полезная лемма без названия (рис. 7)
Внутри треугольника ABC выбрана точка R. Касательная к (BRC) пересекает стороны AB и AC в точках P и Q соответственно. Точка Х находится на дуге BC, не содержащей точку А. Утверждается, что (PXQ) касается (ABC) тогда и только тогда, когда ∠BAC + ∠PXQ = ∠BRC
Узнал про неё отсюда.
Начнем небольшую серию постов, в которой рассмотрим полезные мысли и леммы, помогающие доказывать касание окружностей, и научимся их применять
Мысли:
1. Чаще всего точка касания угадывается. Почти всегда причиной касания является то, что нужные нам окружности просто всегда имеют хорошую общую точку, но нам повезло, и углы такие, что окружности коснулись. А как искать хорошую точку на описанной окружности треугольника? Например, можно взять 3 прямые, содержащие стороны этого треугольника, добавить к ним четвертую прямую и рассмотреть точку Микеля этой четвёрки. Через неё как раз пройдёт 4 окружности, которые помогут поперекидывать углы. Только четвёртую прямую нужно выбирать более менее нормальную.
*Ещё иногда точкой касания является антиштейнер какой то хорошей прямой. Если нет явно заданной прямой через Н, то антиштейнер прямой заданного направления. Вайб такого случая это отражения точек/прямых относительно сторон базового треугольника или явная прямая через Н.
2. Также бывает более глубокая причина касания окружностей, чем уголки. Иногда можно получить касающиеся окружности из уже касающихся объектов на рисунке с помощью поворотной гомотетии или инверсии.
3. Можно попробовать найти на картинке теорему Фейербаха (или какие-то другие известные касания).
Леммы:
1. Слабая теорема Кейси (Кузи) (рис. 1)
Пусть на плоскости даны окружность ω и три точки A, B, C вне неё, не лежащие на одной прямой. Обозначим
длины отрезков касательных из точек A, B, C к окружности ω через ta, tb, tc соответственно. Тогда окружность (ABC) касается окружности ω тогда и только тогда, когда для некоторой расстановки знаков выполнено соотношение
±taBC ± tbCA ± tcAB = 0
Полезно, когда считаются отрезки или явно фигурируют касательные.
2. Очев лемма (рис. 2)
Окружности касаются тогда только тогда, когда Сумма/разность радусов = расстояние между их центрами.
Работает, когда ничего больше не работает. Обычно в таких задачах удобно считаются радиусы окружностей.
3. Лемма о сегменте (рис. 3)
Точка I – инцентр треугольника ABC. Окружность ω с центром в точке O проходит через вершины B и C. Точка Х на AB такова, что ∠BXI = ¼∠BOC. Тогда окружность, вписанная в угол A и касающаяся стороны АВ в точке X, касается ω.
4. Лемма Саваямы (рис. 4)
На стороне BC треугольника ABC выбрана точка X. Тогда окружность, вписанная в угол BXA и касающаяся его сторон в точках P и Q, касается (ABC) тогда и только тогда, когда PQ содержит инцентр (или эксцентр) треугольника АВС.
Полезно подумать о том, что точка Х выбрана не совсем "симметрично". И получить ещё несколько фактов.
5. Лемма с изогоналями (обобщение леммы Архимеда) (рис. 5-6)
Иногда удобнее доказывать изогональность или что какая-то прямая является биссектрисой (например, с помощью счета отрезков), вместо того, чтобы искать угол между касательной и хордой.
Ещё у неё есть прикольное обобщение.
6. Полезная лемма без названия (рис. 7)
Внутри треугольника ABC выбрана точка R. Касательная к (BRC) пересекает стороны AB и AC в точках P и Q соответственно. Точка Х находится на дуге BC, не содержащей точку А. Утверждается, что (PXQ) касается (ABC) тогда и только тогда, когда ∠BAC + ∠PXQ = ∠BRC
Узнал про неё отсюда.
BY Ботаем геому
Share with your friend now:
group-telegram.com/botgeom/328
