как получить случайное разбиение фигуры на доминошки?
можно попробовать начать с какого-то фиксированного разбиения (например, со всеми горизонтальными доминошками), а дальше применять случайные флипы: выбираем случайный квадрат 2×2 в фигуре, если он разбит на две доминошки, делаем флип (= <-> ||)
(задача: 1) доказать, что флипами можно дойти от любого разбиения квадрата на доминошки до любого другого; 2) придумать фигуру, для разбинений которой на доминошки такое неверно)
на первой картинке для квадрата 20×20 без угла сделано 100 флипов и видно, что мы пока от начального разбиения недалеко ушли; на второй картинке 10000 флиплов — и это выглядит уже довольно хаотично
вроде все ожидаемо, ничего особо интересного
...
попробуем теперь то же самое сделать с ацтекским брильянтом порядка 20… ну первый сюрприз, что после 10 тыс. флипов не происходит почти ничего… это, впрочем, не удивительно, в начале даже подходящих квадратов совсем мало…
картинки с брильянтами и продолжение — в следующем посте
===
способ хранения разбиения из предыдущего поста оказался неудобным тем, что значок не говорит, в какую сторону продолжается покрывающая доминошку клетка — стал хранить в каждой клетке указатель на парную к ней (не в программистском смысле указатель, а один из символов →←↓↑ )
картинки рисую matplotlib'ом (код в комментариях)
каждая доминошка покрывает ровно одну клетку с четной суммой координат — цвет доминошки соответствует тому, в какую сторону из этой клетки продолжается доминошка
можно попробовать начать с какого-то фиксированного разбиения (например, со всеми горизонтальными доминошками), а дальше применять случайные флипы: выбираем случайный квадрат 2×2 в фигуре, если он разбит на две доминошки, делаем флип (= <-> ||)
(задача: 1) доказать, что флипами можно дойти от любого разбиения квадрата на доминошки до любого другого; 2) придумать фигуру, для разбинений которой на доминошки такое неверно)
на первой картинке для квадрата 20×20 без угла сделано 100 флипов и видно, что мы пока от начального разбиения недалеко ушли; на второй картинке 10000 флиплов — и это выглядит уже довольно хаотично
вроде все ожидаемо, ничего особо интересного
...
попробуем теперь то же самое сделать с ацтекским брильянтом порядка 20… ну первый сюрприз, что после 10 тыс. флипов не происходит почти ничего… это, впрочем, не удивительно, в начале даже подходящих квадратов совсем мало…
картинки с брильянтами и продолжение — в следующем посте
===
способ хранения разбиения из предыдущего поста оказался неудобным тем, что значок не говорит, в какую сторону продолжается покрывающая доминошку клетка — стал хранить в каждой клетке указатель на парную к ней (
картинки рисую matplotlib'ом (код в комментариях)
каждая доминошка покрывает ровно одну клетку с четной суммой координат — цвет доминошки соответствует тому, в какую сторону из этой клетки продолжается доминошка
group-telegram.com/compmathweekly/10
Create:
Last Update:
Last Update:
как получить случайное разбиение фигуры на доминошки?
можно попробовать начать с какого-то фиксированного разбиения (например, со всеми горизонтальными доминошками), а дальше применять случайные флипы: выбираем случайный квадрат 2×2 в фигуре, если он разбит на две доминошки, делаем флип (= <-> ||)
(задача: 1) доказать, что флипами можно дойти от любого разбиения квадрата на доминошки до любого другого; 2) придумать фигуру, для разбинений которой на доминошки такое неверно)
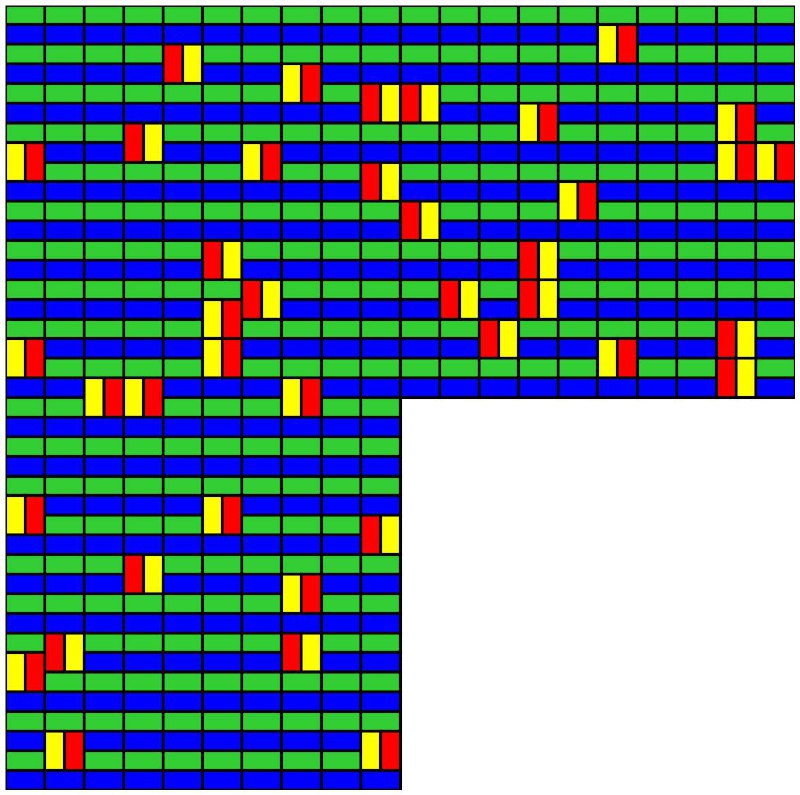
на первой картинке для квадрата 20×20 без угла сделано 100 флипов и видно, что мы пока от начального разбиения недалеко ушли; на второй картинке 10000 флиплов — и это выглядит уже довольно хаотично
вроде все ожидаемо, ничего особо интересного
...
попробуем теперь то же самое сделать с ацтекским брильянтом порядка 20… ну первый сюрприз, что после 10 тыс. флипов не происходит почти ничего… это, впрочем, не удивительно, в начале даже подходящих квадратов совсем мало…
картинки с брильянтами и продолжение — в следующем посте
===
способ хранения разбиения из предыдущего поста оказался неудобным тем, что значок не говорит, в какую сторону продолжается покрывающая доминошку клетка — стал хранить в каждой клетке указатель на парную к ней (не в программистском смысле указатель, а один из символов →←↓↑ )
картинки рисую matplotlib'ом (код в комментариях)
каждая доминошка покрывает ровно одну клетку с четной суммой координат — цвет доминошки соответствует тому, в какую сторону из этой клетки продолжается доминошка
можно попробовать начать с какого-то фиксированного разбиения (например, со всеми горизонтальными доминошками), а дальше применять случайные флипы: выбираем случайный квадрат 2×2 в фигуре, если он разбит на две доминошки, делаем флип (= <-> ||)
(задача: 1) доказать, что флипами можно дойти от любого разбиения квадрата на доминошки до любого другого; 2) придумать фигуру, для разбинений которой на доминошки такое неверно)
на первой картинке для квадрата 20×20 без угла сделано 100 флипов и видно, что мы пока от начального разбиения недалеко ушли; на второй картинке 10000 флиплов — и это выглядит уже довольно хаотично
вроде все ожидаемо, ничего особо интересного
...
попробуем теперь то же самое сделать с ацтекским брильянтом порядка 20… ну первый сюрприз, что после 10 тыс. флипов не происходит почти ничего… это, впрочем, не удивительно, в начале даже подходящих квадратов совсем мало…
картинки с брильянтами и продолжение — в следующем посте
===
способ хранения разбиения из предыдущего поста оказался неудобным тем, что значок не говорит, в какую сторону продолжается покрывающая доминошку клетка — стал хранить в каждой клетке указатель на парную к ней (
картинки рисую matplotlib'ом (код в комментариях)
каждая доминошка покрывает ровно одну клетку с четной суммой координат — цвет доминошки соответствует тому, в какую сторону из этой клетки продолжается доминошка
BY Компьютерная математика Weekly

Share with your friend now:
group-telegram.com/compmathweekly/10
