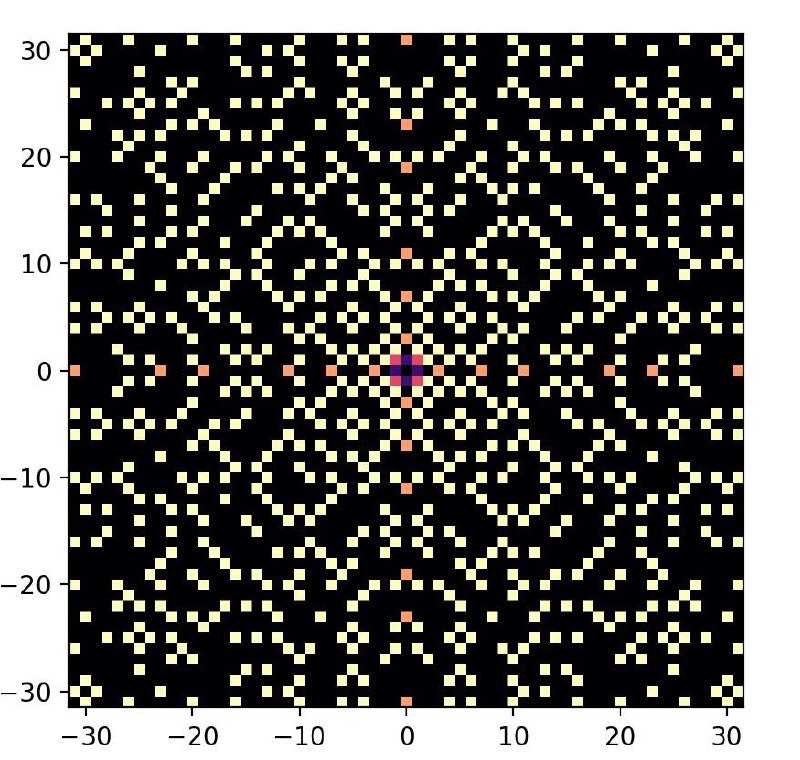
в промежутке между разным — нарисовал картинку с простыми числами в Z[i]
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
group-telegram.com/compmathweekly/31
Create:
Last Update:
Last Update:
в промежутке между разным — нарисовал картинку с простыми числами в Z[i]
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
BY Компьютерная математика Weekly

Share with your friend now:
group-telegram.com/compmathweekly/31
