Сегодня состоялась устная олимпиада по геометрии 📐 Делимся условиями олимпиады 🔥

А задачи и итоги тура вы, как всегда, можете обсудить в комментах 👇

Задача. Четырехугольник 𝐴𝐵𝐶𝐷, противолежащие стороны которого не параллельны, вписан в окружность. Пусть 𝑋𝑌 — произвольный диаметр этой окружности, 𝑃 — проекция точки 𝑋 на прямую 𝐴𝐵, 𝑄 — проекция точки 𝑌 на прямую 𝐶𝐷. Найдите ГМТ середин отрезков 𝑃𝑄.

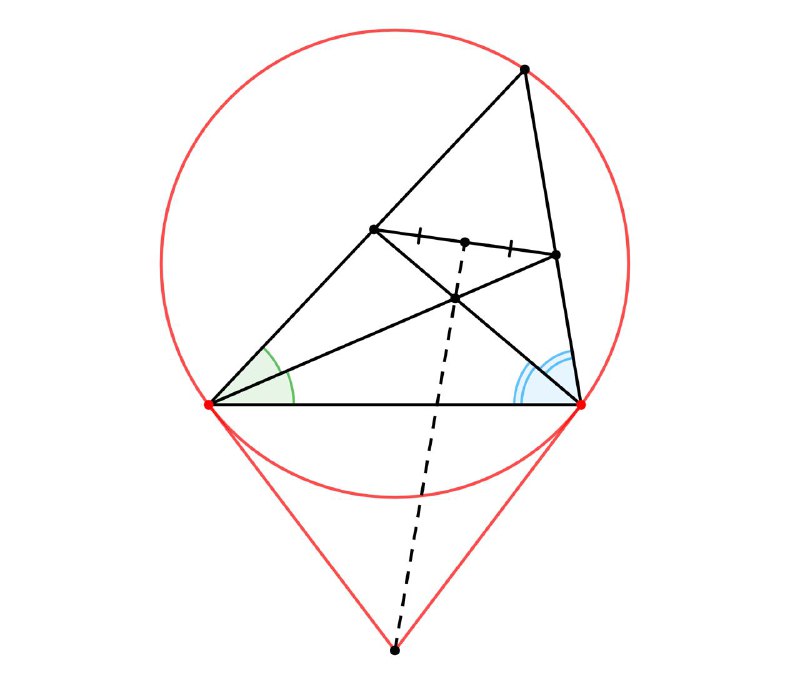
Задача. В треугольнике 𝐴𝐵𝐶 биссектрисы 𝐵𝐹 и 𝐶𝐸 пересекаются в точке 𝐼, 𝐺 — середина 𝐸𝐹 , 𝐾 — точка пересечения касательных к описанной окружности треугольника 𝐴𝐵𝐶, проведенных в точках 𝐵 и 𝐶. Докажите, что точки 𝐾, 𝐼 и 𝐺 лежат на одной прямой.