group-telegram.com/thirdwavedev/137
Last Update:
Пригадую, як на першому курсі, коли ми проходили вступ до комп’ютерної інженерії, один із викладачів пояснював тему дискретизації сигналу. Одне з правил, яке він розповів, звучало приблизно так: «частота дискретизації має бути щонайменше вдвічі більшою за частоту сигналу».
На жаль (а може й на щастя), часу курсу не вистачало, щоб дуже глибоко зрозуміти всі аспекти цієї теми, ну а ще й я не був найздібнішим студентом. Тим не менш, інколи мені це згадується. А недавно мені в рекомендаціях трапилося відео, де більш наочно пояснено, що ж це взагалі таке.
https://www.youtube.com/watch?v=eBHbCZo9QrM
Одразу поясню, чому я про це пишу. На мою думку, розуміння таких тем загалом не потрібне для веб-розробки. Але я також вірю, що хоча б поверхневе розуміння того, як працює комп’ютер загалом, є важливим і додає вам певного % конкурентоспроможності. Тому я інколи кидаю щось і про embedded, роботу з пам’яттю чи те, як працює операційна система.
Сигнали є всюди: звук, зображення, будь-які дані — все це передається у вигляді аналогових сигналів. Комп’ютери дискретні, тобто працюють із визначеним набором значень, ну типу 0 та 1. Сигнали ж аналогові. І щоб перетворити сигнал з аналогу на дискретний, використовують семплінг: з певною частотою «слухають» вхідний сигнал і перетворюють його амплітуду в точках семплінгу на якісь дискретні значення.
Але щоб отримати цілісні дані, нам потрібно вибрати частоту, з якою цей семплінг відбувається, — тобто частоту дискретизації. Це сама по собі складна тема, не думаю, що зміг би докладно пояснити, бо сам не маю глибоких знань. Але тут достатньо згадати правило, про яке я писав вище: частота дискретизації має бути принаймні вдвічі вищою за частоту сигналу.
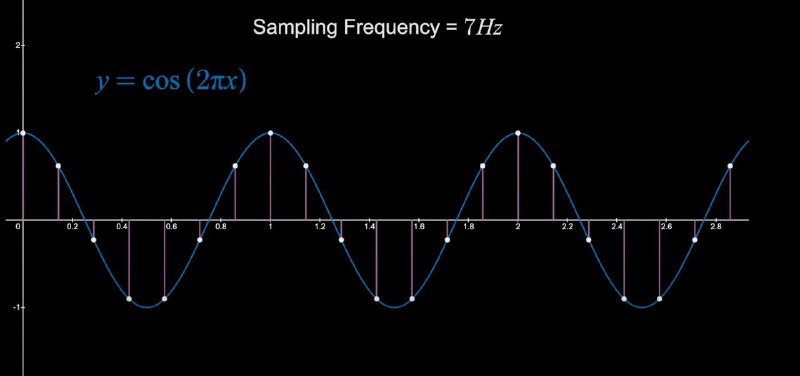
Уявімо сигнал частотою X герц, синусоїду, наприклад. Щоб перетворити його на дискретні значення, нам недостатньо частоти дискретизації теж X герц, адже тоді ми втратимо половину вершин сигналу. Мінімум нам потрібно 2 X герц, щоб дискретні значення відображали всі вершини. При нижчих частотах семплінгу спостерігається спотворення (aliasing), коли сигнал набуває хибного вигляду й не відтворює справжню форму. Тож правило «вдвічі більшої частоти» дійсно гарантує, що ключові точки сигналу «ловляться» без втрат.
Це ще називається теоремою Віттекера — Найквіста — Котельникова — Шеннона. Пригадую з універу тільки прізвище Шеннона.
А знаєте, як його звали? Клод Шеннон (Claude Shannon). Вікіпедія спекулює, що це ім’я взяли для назви відомої LLM-моделі, але переконливих підтверджень я не знайшов
BY Розробка третьої хвилі
Share with your friend now:
group-telegram.com/thirdwavedev/137
