В прошлый раз мы говорили о размере орбиты. Сегодня мы перейдем к обсуждению формы орбиты и первый раз затронем ситуацию, когда орбита перестает быть замкнутой.
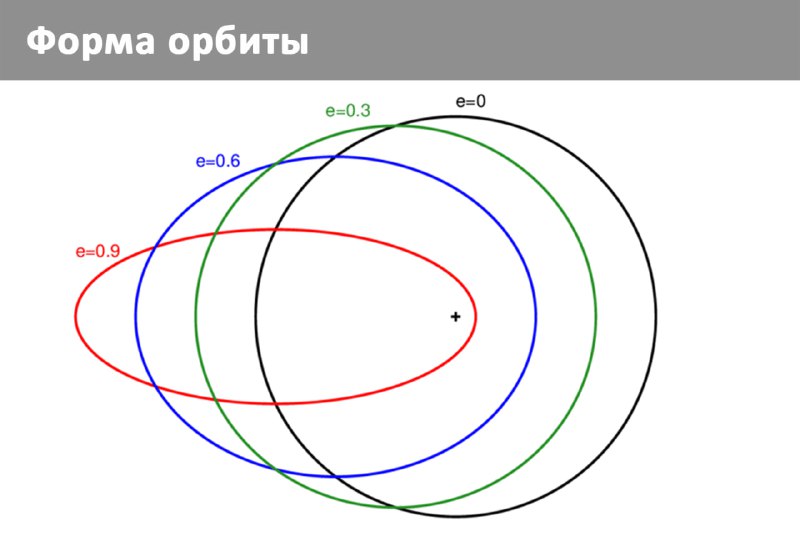
Замкнутая орбита имеет форму эллипса, в частности, окружности. Форму эллипса можно характеризовать через соотношение его большой и малой полуоси: чем первая больше другой, тем более вытянут эллипс. Когда они совпадают, эллипс совпадает с окружностью, а большая полуось – с радиусом окружности.
Но есть куда более удобная возможность оценить форму орбиты: математика позволяет вывести из уравнения движения тела в центральном поле параметр, который называется эксцентриситет (обозначается латинской буквой «e»).
Это величина, которая может принимать значения от нуля до бесконечности и показывает, насколько форма орбиты отличается от окружности:
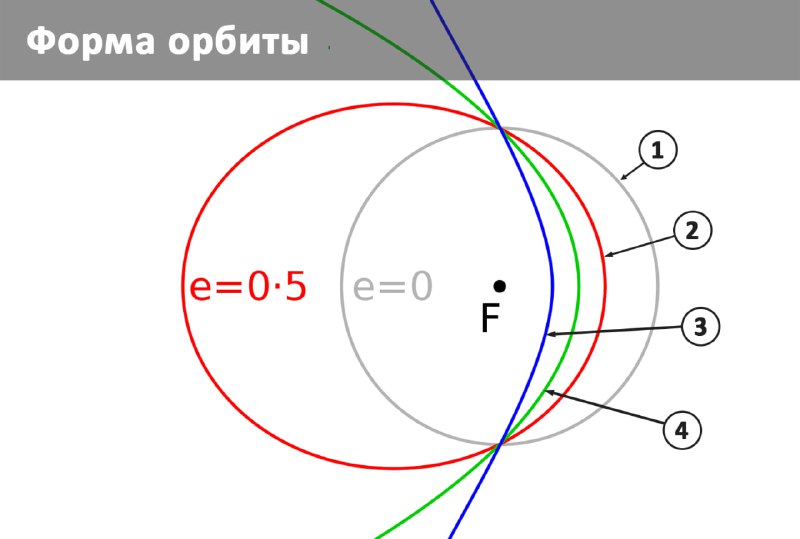
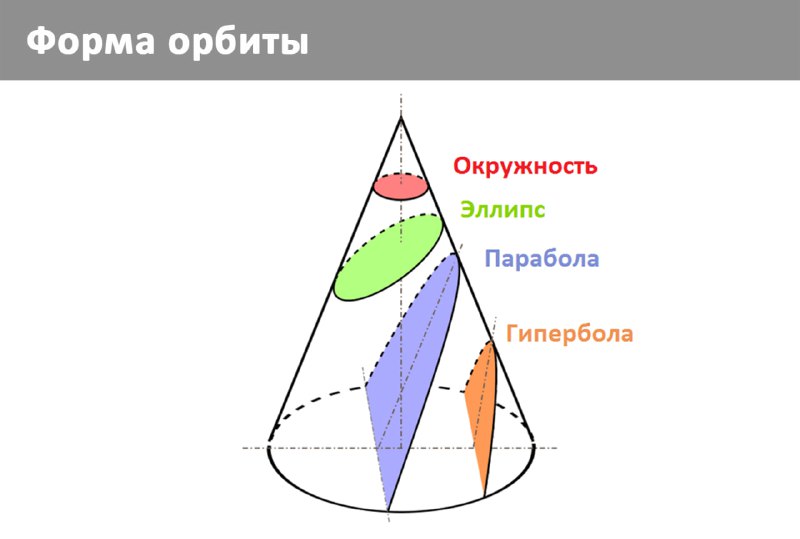
Если эксцентриситет равен нулю (e = 0), то орбита – окружность ❶
Если эксцентриситет больше нуля и меньше единицы (0 < e < 1) – это все более и более вытянутый эллипс ❷.
Если апоцентр эллиптической орбиты выходит за пределы сферы Хилла*, то уже нельзя говорить о том, что орбита остается замкнутой. Это соответствует моменту, когда эксцентриситет становится больше или равен единице:
Если эксцентриситет достиг значения 1 (e = 1) – то орбита перестала быть замкнутой и имеет форму параболы ❹
Если эксцентриситет больше 1 (e > 1) – орбита стала гиперболой ❸ (и чем больше эксцентриситет, тем более разомкнуты ветви гиперболы, в пределе стремясь стать прямой).
И для параболы, и для гиперболы значение большой полуоси будет отрицательным, а радиус апоцентра – равным бесконечности, и говорить об их размере затруднительно.
Все перечисленные формы орбит являются коническими сечениями. В реальном мире невозможно найти ситуацию, когда объект движется точно по траекториям, которые можно описать такими идеальными орбитами, но они подходят, как начальное приближение или оценка траектории на короткое время (оскулирующая орбита).
* - при старте с поверхности этому соответствует набор второй космической скорости.
#орбитальнаямеханика
Замкнутая орбита имеет форму эллипса, в частности, окружности. Форму эллипса можно характеризовать через соотношение его большой и малой полуоси: чем первая больше другой, тем более вытянут эллипс. Когда они совпадают, эллипс совпадает с окружностью, а большая полуось – с радиусом окружности.
Но есть куда более удобная возможность оценить форму орбиты: математика позволяет вывести из уравнения движения тела в центральном поле параметр, который называется эксцентриситет (обозначается латинской буквой «e»).
Это величина, которая может принимать значения от нуля до бесконечности и показывает, насколько форма орбиты отличается от окружности:
Если эксцентриситет равен нулю (e = 0), то орбита – окружность ❶
Если эксцентриситет больше нуля и меньше единицы (0 < e < 1) – это все более и более вытянутый эллипс ❷.
Если апоцентр эллиптической орбиты выходит за пределы сферы Хилла*, то уже нельзя говорить о том, что орбита остается замкнутой. Это соответствует моменту, когда эксцентриситет становится больше или равен единице:
Если эксцентриситет достиг значения 1 (e = 1) – то орбита перестала быть замкнутой и имеет форму параболы ❹
Если эксцентриситет больше 1 (e > 1) – орбита стала гиперболой ❸ (и чем больше эксцентриситет, тем более разомкнуты ветви гиперболы, в пределе стремясь стать прямой).
И для параболы, и для гиперболы значение большой полуоси будет отрицательным, а радиус апоцентра – равным бесконечности, и говорить об их размере затруднительно.
Все перечисленные формы орбит являются коническими сечениями. В реальном мире невозможно найти ситуацию, когда объект движется точно по траекториям, которые можно описать такими идеальными орбитами, но они подходят, как начальное приближение или оценка траектории на короткое время (оскулирующая орбита).
* - при старте с поверхности этому соответствует набор второй космической скорости.
#орбитальнаямеханика
group-telegram.com/explaining_space/35
Create:
Last Update:
Last Update:
В прошлый раз мы говорили о размере орбиты. Сегодня мы перейдем к обсуждению формы орбиты и первый раз затронем ситуацию, когда орбита перестает быть замкнутой.
Замкнутая орбита имеет форму эллипса, в частности, окружности. Форму эллипса можно характеризовать через соотношение его большой и малой полуоси: чем первая больше другой, тем более вытянут эллипс. Когда они совпадают, эллипс совпадает с окружностью, а большая полуось – с радиусом окружности.
Но есть куда более удобная возможность оценить форму орбиты: математика позволяет вывести из уравнения движения тела в центральном поле параметр, который называется эксцентриситет (обозначается латинской буквой «e»).
Это величина, которая может принимать значения от нуля до бесконечности и показывает, насколько форма орбиты отличается от окружности:
Если эксцентриситет равен нулю (e = 0), то орбита – окружность ❶
Если эксцентриситет больше нуля и меньше единицы (0 < e < 1) – это все более и более вытянутый эллипс ❷.
Если апоцентр эллиптической орбиты выходит за пределы сферы Хилла*, то уже нельзя говорить о том, что орбита остается замкнутой. Это соответствует моменту, когда эксцентриситет становится больше или равен единице:
Если эксцентриситет достиг значения 1 (e = 1) – то орбита перестала быть замкнутой и имеет форму параболы ❹
Если эксцентриситет больше 1 (e > 1) – орбита стала гиперболой ❸ (и чем больше эксцентриситет, тем более разомкнуты ветви гиперболы, в пределе стремясь стать прямой).
И для параболы, и для гиперболы значение большой полуоси будет отрицательным, а радиус апоцентра – равным бесконечности, и говорить об их размере затруднительно.
Все перечисленные формы орбит являются коническими сечениями. В реальном мире невозможно найти ситуацию, когда объект движется точно по траекториям, которые можно описать такими идеальными орбитами, но они подходят, как начальное приближение или оценка траектории на короткое время (оскулирующая орбита).
* - при старте с поверхности этому соответствует набор второй космической скорости.
#орбитальнаямеханика
Замкнутая орбита имеет форму эллипса, в частности, окружности. Форму эллипса можно характеризовать через соотношение его большой и малой полуоси: чем первая больше другой, тем более вытянут эллипс. Когда они совпадают, эллипс совпадает с окружностью, а большая полуось – с радиусом окружности.
Но есть куда более удобная возможность оценить форму орбиты: математика позволяет вывести из уравнения движения тела в центральном поле параметр, который называется эксцентриситет (обозначается латинской буквой «e»).
Это величина, которая может принимать значения от нуля до бесконечности и показывает, насколько форма орбиты отличается от окружности:
Если эксцентриситет равен нулю (e = 0), то орбита – окружность ❶
Если эксцентриситет больше нуля и меньше единицы (0 < e < 1) – это все более и более вытянутый эллипс ❷.
Если апоцентр эллиптической орбиты выходит за пределы сферы Хилла*, то уже нельзя говорить о том, что орбита остается замкнутой. Это соответствует моменту, когда эксцентриситет становится больше или равен единице:
Если эксцентриситет достиг значения 1 (e = 1) – то орбита перестала быть замкнутой и имеет форму параболы ❹
Если эксцентриситет больше 1 (e > 1) – орбита стала гиперболой ❸ (и чем больше эксцентриситет, тем более разомкнуты ветви гиперболы, в пределе стремясь стать прямой).
И для параболы, и для гиперболы значение большой полуоси будет отрицательным, а радиус апоцентра – равным бесконечности, и говорить об их размере затруднительно.
Все перечисленные формы орбит являются коническими сечениями. В реальном мире невозможно найти ситуацию, когда объект движется точно по траекториям, которые можно описать такими идеальными орбитами, но они подходят, как начальное приближение или оценка траектории на короткое время (оскулирующая орбита).
* - при старте с поверхности этому соответствует набор второй космической скорости.
#орбитальнаямеханика
BY Объясняем просто: космос
Share with your friend now:
group-telegram.com/explaining_space/35
