Новогодняя подборка про #календарь
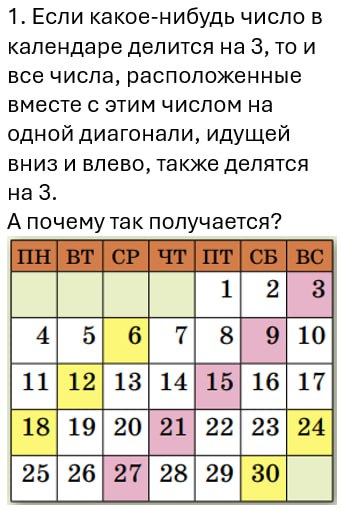
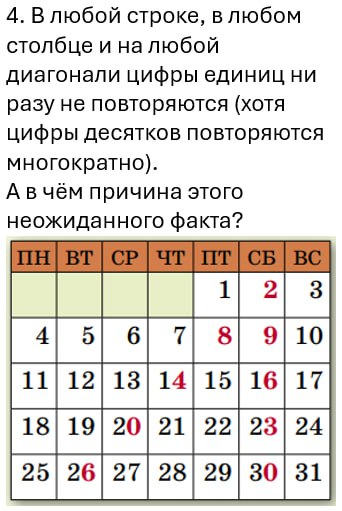
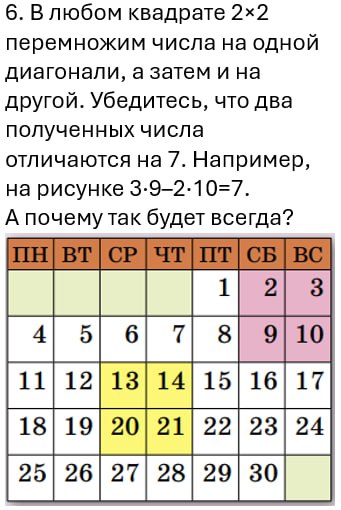
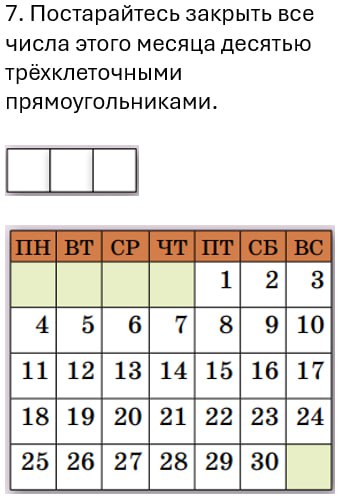
Снимая старые календари, вешая новые, обратите внимание на свойства календарей. Про задачи 7 и 8 поисследуйте: какие месяцы можно разделить на прямоугольники из трех клеток, а какие нельзя.
Источник: статья «Календарь» (Лейб Штейнгарц, Квантик №5, 2012)
Кстати, на сайте журнала в архиве выложены все номера, кроме последнего полугодия.
Задачу №9 из этой подборки я придумала когда-то в 2006 году для Математического праздника
Если доказывать предложенные закономерности, то это класса с 6-го и старше. А помладше — пронаблюдайте, не доказывая.
Снимая старые календари, вешая новые, обратите внимание на свойства календарей. Про задачи 7 и 8 поисследуйте: какие месяцы можно разделить на прямоугольники из трех клеток, а какие нельзя.
Источник: статья «Календарь» (Лейб Штейнгарц, Квантик №5, 2012)
Кстати, на сайте журнала в архиве выложены все номера, кроме последнего полугодия.
Задачу №9 из этой подборки я придумала когда-то в 2006 году для Математического праздника
Если доказывать предложенные закономерности, то это класса с 6-го и старше. А помладше — пронаблюдайте, не доказывая.
group-telegram.com/printtask/132
Create:
Last Update:
Last Update:
Новогодняя подборка про #календарь
Снимая старые календари, вешая новые, обратите внимание на свойства календарей. Про задачи 7 и 8 поисследуйте: какие месяцы можно разделить на прямоугольники из трех клеток, а какие нельзя.
Источник: статья «Календарь» (Лейб Штейнгарц, Квантик №5, 2012)
Кстати, на сайте журнала в архиве выложены все номера, кроме последнего полугодия.
Задачу №9 из этой подборки я придумала когда-то в 2006 году для Математического праздника
Если доказывать предложенные закономерности, то это класса с 6-го и старше. А помладше — пронаблюдайте, не доказывая.
Снимая старые календари, вешая новые, обратите внимание на свойства календарей. Про задачи 7 и 8 поисследуйте: какие месяцы можно разделить на прямоугольники из трех клеток, а какие нельзя.
Источник: статья «Календарь» (Лейб Штейнгарц, Квантик №5, 2012)
Кстати, на сайте журнала в архиве выложены все номера, кроме последнего полугодия.
Задачу №9 из этой подборки я придумала когда-то в 2006 году для Математического праздника
Если доказывать предложенные закономерности, то это класса с 6-го и старше. А помладше — пронаблюдайте, не доказывая.
BY Золотая задача






Share with your friend now:
group-telegram.com/printtask/132
