group-telegram.com/ansi_logic/242
Last Update:
Задачу, о которой я хочу рассказать, давали на межнаре в 2010 году. У этой задачи супер-простая формулировка, и при этом задача тесно связана с логикой (точнее, с теорией алгоритмов), что для математических олимпиад в целом редкость! Увы, задачи по логике обычно дают только самым маленьким, и в основном это что-то про рыцарей и лжецов. Для меня было радостно узнать, что логика встретилась на олимпиаде для больших, причём на такой серьёзной олимпиаде! Если вам вдруг известны другие логические задачи с олимпиад для больших, сообщите, пожалуйста! О них я тоже с удовольствием расскажу ☺
Условие задачи межнара таково. Есть 6 стопок с монетами, в каждой стопке изначально лежит по 1 монетке. Разрешается делать следующие действия:
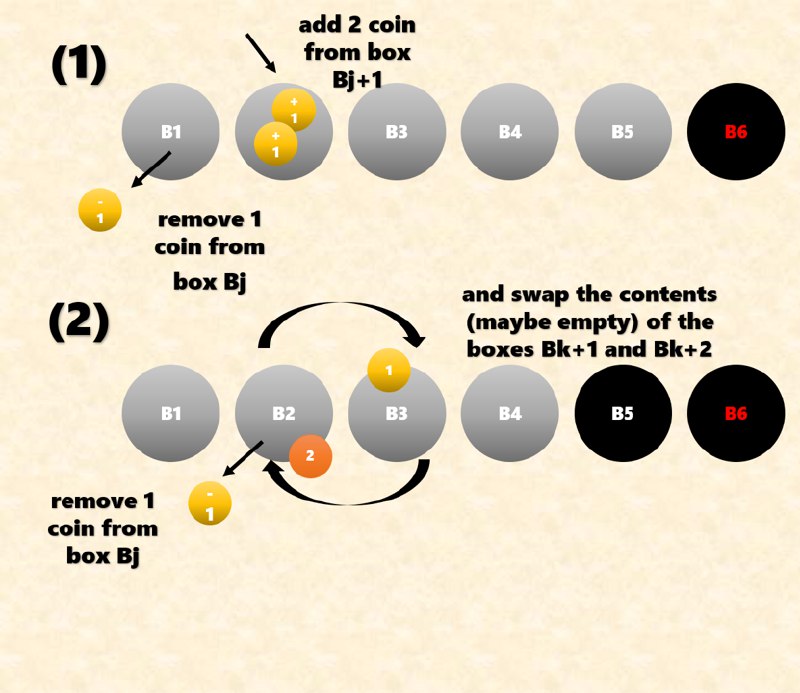
- убрать монету из k-ой стопки и добавить 2 монеты в k+1-ю стопку;
- убрать монету из k-ой стопки и поменять местами k+1-ю и k+2-ю стопки.
Нужно выяснить, можно ли сделать такое: все стопки, кроме шестой, пусты, а шестая содержит огромную кучу монет! А именно, 2010^2010^2010.
Задача выглядит весьма невинно, и непонятно, как можно сделать огромную кучу монет такими простыми операциями. Скажу спойлер, что можно, но детали раскрывать не буду, чтобы не лишать вас удовольствия порешать. Разумеется, конкретное число 2010^2010^2010 роли не играет, оно лишь отражает год олимпиады и оно большое, вот и всё.
При чём же тут теория алгоритмов? Если у нас изначально не 6 стопок, а сколь угодно много (и в них что-то лежит, например, в самой левой несколько монет, а остальные пусты), то такими перекладываниями можно сымитировать вычисление функции типа быстрорастущей функции Аккермана! У функции Аккермана есть разные варианты определений, но все они растут примерно одинаково быстро. Я так поняла, что здесь тоже получается функция подобного роста.
Подробнее про эту задачу можно почитать здесь.
BY Анси логика
Share with your friend now:
group-telegram.com/ansi_logic/242
