group-telegram.com/olympgeom/1406
Last Update:
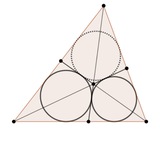
Какие еще есть доказательства теоремы Монжа?
Ну, во-первых, есть стандартное доказательство с теоремой Менелая. Я бы даже сказал, что теорема Монжа это и есть теорема Менелая.
Во-вторых, есть доказательство с композицией гомотетий. Если композиция трех гомотетий является тождественным преобразованием, то центры лежат на одной прямой. Как это понять? Надо проследить, например, за центром первой гомотетии. Если центры гомотетий не лежат на одной прямой, то он не имеет шансов вернуться назад в исходное положение.
В-третьих, есть замечательное доказательство от Григория Мерзона с линейными функциями. Обозначим центры окружностей A, B, C, их радиусы — a, b, c. Пускай [B,C] — линейная функция на плоскости, которая в точках B и C равна 0, а в точке A равна 1 (в частности, [B,C]=0 — уравнение линии центров этих окружностей). Аналогично определим функции [C,A] и [A,B].
Тогда a[B,C]+b[C,A]+c[A,B]=0 — уравнение прямой, на которой лежат нужные три точки.
В-четвертых, есть доказательство с моделью Пуанкаре плоскости Лобачевского. Вкратце, если радиусы (в смысле модели) первой и второй окружностей равны, и второй и третьей равны, то и радиусы первой и третей окружностей равны. А движение, переводящее равные окружности друг в друга это как раз гомотетия с центром на абсолюте.
В-пятых, есть доказательство Акопяна из вчерашнего поста.
А в-шестых, предлагаю такое доказательство с помощью масс. Пусть опять центры окружностей A, B, C, их радиусы — a, b, c. Поставим в точку A массу b-c, в точку B массу c-a, и в точку C массу a-b. Сумма масс равна нулю, центра масс нет, но есть утверждение, которое я называю лемма о диполе
Предположим дана система материальных точек с нулевой суммой масс. Ее разбили на две группы двумя способами. При первом разбиении образовалось две группы с ненулевыми суммами, при этом группа с положительной суммой масс имеет центром точку X+, а группа с отрицательной суммой масс имеет центром точку X-. При втором разбиении аналогично получаются точки Y+ и Y-. Тогда X-X+ и Y-Y+ параллельны - дипольная ось.
В нашем случае мы разобьем, скажем, массу в точке C на две
a-b=a/c(c-b)+b/c(a-c)
массы (A, b-c) и (C, a/c(c-b)) группируются в центр гомотетии окружностей с центрами A и C;
массы (B, c-a), (C, b/c(a-c)) группируются в центр гомотетии окружностей с центрами B и C;
поэтому прямая, соединяющая два центра гомотетий, параллельна дипольной оси нашей системы масс. а значит и все три центра лежат на одной прямой.
UPD. Забыл еще доказательство со сферами и выходом в пространство..
BY Олимпиадная геометрия
Warning: Undefined variable $i in /var/www/group-telegram/post.php on line 260
Share with your friend now:
group-telegram.com/olympgeom/1406