group-telegram.com/ansi_logic/436
Last Update:
Любой математический объект be like: "а вы бы меня изучали, если бы я не существовал? 🥺"
Сегодня наткнулась на нечто удивительное... в двух словах: проникновение огромных кардиналов, существование которых (вроде как) не выводится в ZFC, в конечную математику натуральных чисел 😱
Теперь подробнее (тут есть ссылки на статьи). Рассмотрим бинарную операцию * на натуральных числах от 1 до 2^n, удовлетворяющую двум условиям:
1) a*1 = (a+1) mod (2^n)
2) a*(b*c)=(a*b)*(a*c)
Теперь через P(n) обозначим период последовательности 1*1, 1*2, ..., 1*(2^n). И тут начинаются странности 😳
Последовательность P(n) выглядит так: 1, 1, 2, 4, 4, 8, 8, 8, 8, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16,....
Последовательность P(n) состоит только из степеней двоек. Как оказалось, число 32 точно не возникнет вплоть до A(9,A(8,A(8,255)))-го места (где А - дикорастующая функция Аккермана). Неизвестно, можно ли доказать, что где-то в этой последовательности есть 32, если использовать только ZFC. Однако, если предположить существование некоторого огроменного кардинала, то можно доказать неограниченность этой последовательности 😨
Закончу словами негативщика, пост которого мне недавно любезно прислали в комментариях: "Но практически никто в математических трудах (я даже исключений не припомню) не ссылается хотя бы на какие-то логические факты. Ни в какой теореме логические факты не нужны! Всё прекрасно развивается без логики, и логика нигде никому не помогает!"
BY Анси логика
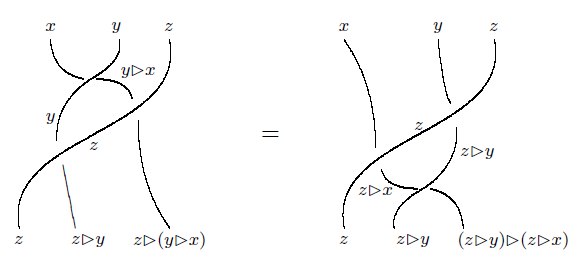
Share with your friend now:
group-telegram.com/ansi_logic/436
